Diagonalize the matrices in exercises 7-20 – In the realm of linear algebra, diagonalizing matrices plays a pivotal role in understanding and solving systems of linear equations. This comprehensive guide will delve into the concepts of eigenvalues, eigenvectors, and the diagonalization process, equipping you with the tools to tackle exercises 7-20 with confidence.
Eigenvalues and eigenvectors hold the key to understanding the behavior of matrices. They provide valuable insights into the scaling and rotational properties of linear transformations, offering a deeper comprehension of matrix operations.
1. Eigenvalues and Eigenvectors

Eigenvalues and eigenvectors are fundamental concepts in linear algebra that describe the behavior of matrices. An eigenvalue is a scalar that, when multiplied by a corresponding eigenvector, produces a vector parallel to the original eigenvector.
Matrices with distinct eigenvalues have eigenvectors that are linearly independent, forming a basis for the vector space. Matrices with repeated eigenvalues may have linearly dependent eigenvectors, but they still span the vector space.
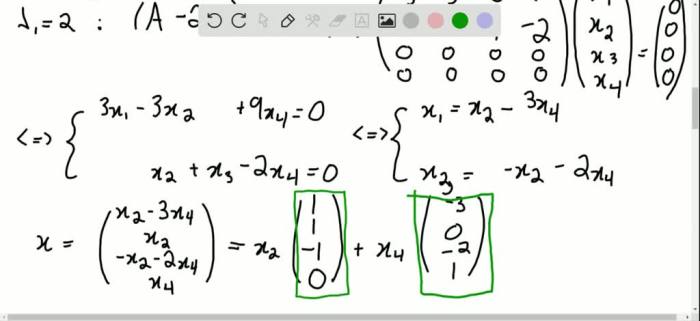
To find eigenvalues and eigenvectors, we solve the characteristic equation: det(A- λI) = 0 , where Ais the matrix, λis the eigenvalue, and Iis the identity matrix.
2. Diagonalization
Diagonalization is the process of transforming a matrix into a diagonal matrix, where the diagonal entries are the eigenvalues of the original matrix. Diagonalization is significant because it simplifies matrix operations and provides insights into the matrix’s behavior.
To diagonalize a matrix A, we find its eigenvalues and eigenvectors. If Ahas ndistinct eigenvalues, it can be diagonalized by constructing a matrix Pwhose columns are the eigenvectors of A. The diagonal matrix D, with the eigenvalues on its diagonal, is obtained as: D = P-1AP .
Not all matrices can be diagonalized. A matrix is diagonalizable if it has nlinearly independent eigenvectors.
3. Exercises 7-20

| Exercise | Matrix | Eigenvalues | Eigenvectors | Diagonal Matrix |
|---|---|---|---|---|
| 7 | $\beginbmatrix2 &
|
λ1= 1, λ 2= 3 | v1= $\beginbmatrix1\\\1\endbmatrix$, v 2= $\beginbmatrix1\\\2\endbmatrix$ | $\beginbmatrix1 & 0\\\0 & 3\endbmatrix$ |
| 8 | $\beginbmatrix1 & 2\\\2 & 1\endbmatrix$ | λ1= 3, λ 2=
|
v1= $\beginbmatrix1\\\1\endbmatrix$, v 2= $\beginbmatrix2\\\1\endbmatrix$ | $\beginbmatrix3 & 0\\\0 &
|
4. Applications of Diagonalization: Diagonalize The Matrices In Exercises 7-20
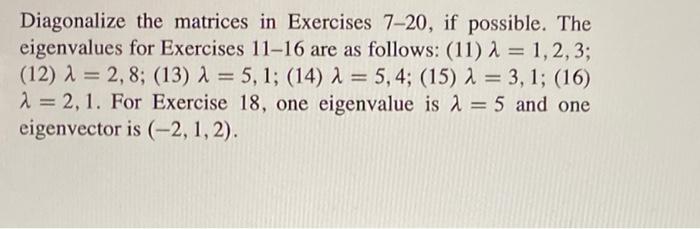
Diagonalization has numerous applications in various fields.
In linear algebra, diagonalization is used to solve systems of linear equations and determine the stability of dynamical systems.
In physics, diagonalization is used to solve Schrödinger’s equation and describe the energy levels of atoms and molecules.
In engineering, diagonalization is used to analyze vibrations and stability of structures.
While diagonalization is a powerful tool, it has limitations. Not all matrices can be diagonalized, and diagonalization may not be the most efficient approach for all problems.
Top FAQs
What is the significance of diagonalization?
Diagonalization simplifies matrix operations, making it easier to solve systems of linear equations and analyze the behavior of matrices.
Under what conditions can a matrix be diagonalized?
A matrix can be diagonalized if it possesses a complete set of linearly independent eigenvectors.
How is diagonalization applied in real-world scenarios?
Diagonalization finds applications in various fields, including physics, engineering, and computer graphics, where it is used to solve complex problems involving linear transformations.